Generic Topological Sort
Intro
Topological sorting comes up often in applications such as task schedulers, dependency resolvers, and node-based computation engines. Let’s try to design and implement generic topological sorting in C++.
Specifically, we want to implement topological_sort with the following signature:
template< class RandomIt, class F >
void topological_sort( RandomIt first, RandomIt last, F edge );
[first, last)denotes a list of vertices.edgeis a callable such that:- If there is an edge from
utov, thenedge(u, v)returnstrue - Otherwise,
edge(u, v)returnsfalse
- If there is an edge from
Can we reuse std::sort?
As a rule of thumb, if there’s something in the standard library that solves our problem, we should preferably use them.
We have a candidate: std::sort (and std::ranges::sort). Its API looks like:
/// Sorts the elements in the range [`first`, `last`) in non-descending order,
/// with respect to a comparator `comp`.
template< class RandomIt, class Compare >
void sort( RandomIt first, RandomIt last, Compare comp );
And what is comp? comp(x, y) returns true if and only if x is “less than” y. This seems to match our edge comparator exactly:
- A Vertex
uis “less than”vif there is an edge fromutov - For example, if the vertices represent tasks, when it means
umust be completed beforev
So, can we simply
template< class RandomIt, class F >
void topological_sort( RandomIt first, RandomIt last, F edge ) {
std::sort(first, last, edge);
}
and call it a day? Does it work?
It Does Not.
Let’s try it with an example. The graph looks like this:
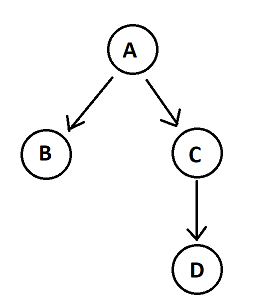
There are exactly 3 topological orderings of the graph:
ABCDACBDACDB
The following program generates all permutations of the vertices, supplies them to std::sort, and shows the output:
#include <algorithm>
#include <iostream>
#include <string>
int main() {
std::string vertices{'A', 'B', 'C', 'D'};
auto edge = [](char u, char v) {
return (u == 'A' && v == 'B')
|| (u == 'A' && v == 'C')
|| (u == 'C' && v == 'D')
;
};
do {
auto sorted = vertices;
std::sort(sorted.begin(), sorted.end(), edge);
std::cout << vertices << " --> " << sorted << '\n';
} while (std::next_permutation(vertices.begin(), vertices.end()));
}
Compiled using GCC 13.1.0, the above program prints:
ABCD --> ABCD
ABDC --> ABCD
ACBD --> ACBD
ACDB --> ACDB
ADBC --> ADBC
ADCB --> ACDB
BACD --> ABCD
BADC --> ABCD
BCAD --> ABCD
BCDA --> ABCD
BDAC --> ABCD
BDCA --> ABCD
CABD --> ACBD
CADB --> ACDB
CBAD --> ACBD
CBDA --> ACBD
CDAB --> ACDB
CDBA --> ACDB
DABC --> CDAB
DACB --> CDAB
DBAC --> CDAB
DBCA --> ACDB
DCAB --> ACDB
DCBA --> ACDB
As we can see, there are 3 cases where the outputs are wrong:
DABC --> CDAB
DACB --> CDAB
DBAC --> CDAB
So what’s going here?
Preconditions of std::sort
As another rule of thumb, if a standard library algorithm, especially a long-lived and well-tested one like std::sort, produces unexpected results, it’s most likely our fault of providing bad inputs - inputs that violate the preconditions.
But in our cases:
- We provided a random-access sequence
- We provided a comparator that matches the required signature
And in fact, in any of the above fails to hold, we would get a hard compile error.
Reading again the the sort documentation, more carefully this time:
comp - comparison function object (i.e. an object that satisfies the requirements of Compare) which returns
trueif the first argument is less than (i.e. is ordered before) the second.
What are the requirements of Compare? In the documentation of Compare, we have this section:
Establishes strict weak ordering relation with the following properties:
- For all
a,comp(a, a) == false.- If
comp(a, b) == truethencomp(b, a) == false.- If
comp(a, b) == trueandcomp(b, c) == truethencomp(a, c) == true.
edge satisfies 1 and 2, but not 3: edge(A, C) == true and edge(C, D) == true, but edge(A, D) == false.
So that must be it, right? We just need to change edge to path and it’ll work?
path(u, v)returns true if and only iff there is a path fromutov(which contains one or more edges)
Hold on a second. There’s another section on equiv(a, b), which is defined as !comp(a, b) && !comp(b, a) (a and b are considered equal if neither precedes the other), as follows:
Establishes equivalence relationship with the following properties: …
- If
equiv(a, b) == trueandequiv(b, c) == true, thenequiv(a, c) == true
This (equivalence relationship) is where the real trouble is.
In our example, equiv(B, C) == true and equiv(B, D) == true, therefore std::sort goes ahead and assumes equiv(C, D) == true, which is incorrect, because C is in fact less than D since there is an edge from C to D. Therefore, even if we replace edge with path, 4 (equivalence relationship) is still violated.
But why is this such a big deal? Why can’t it “just work”?
Let’s forget std::sort for a moment and look at the simpler std::is_sorted. Recall the definition of “sorted sequence” states that every pair is ordered correctly, so there should be O(N^2) checks to be thorough, but std::is_sorted runs in O(N) time. How is that possible?
As you may already know it, std::is_sorted only checks the adjacent pairs. All the rest are inferred, and it is allowed to do so because of the properties of Compare! In our example, std::is_sorted will happily consider DABC “sorted”, while in fact it is not.
In general, any algorithm that requires Compare (read: strict weak ordering), including std::sort, cannot be used to implement topological sorting because the vertices of a directed acyclic graph do not form a strict weak ordering.
What do we do instead?
We may implement topological sort from scratch.
The naive way is to do a modified insertion sort: In each iteration, we find a source - a vertex without any incoming edge, then we put it at the front.
/// topological sort, the brute force
template< class RandomIt, class F >
void topological_sort( RandomIt first, RandomIt last, F edge ) {
for (; first != last; ++first) {
// check if *first is a source.
for (auto other = std::next(first); other != last; ++other) {
if (edge(*other, *first)) {
// *first is not a source; *other may be
std::swap(*other, *first);
// IMPORTANT! have to do the full search again for the new *first
other = first;
}
}
}
}
This is short and concise, requires constant extra memory, but what about the time complexity?
Note that due to the important other = first inside the nested loop,
this solution is O(|V|^3) in time, where |V| is the number of vertices.
Alternatively, we could use Kahn’s algorithm. The rough idea is:
- Put all the sources into a queue
S - Remove a source,
u, fromS, and outputu - Remove all outgoing edges of
u - Some (previous) direct successor of
u,v, may become a source; if so, addvtoS - Go back to step 2 until
Sis empty
/// topological sort, Kahn's algorithm
template< class RandomIt, class F >
void topological_sort( RandomIt first, RandomIt last, F edge ) {
std::size_t n = std::ranges::distance(first, last);
std::vector<std::size_t> in_degree(n);
for (std::size_t i = 0; i < n; ++i) {
for (std::size_t j = 0; j < n; ++j) {
in_degree[i] += bool(edge(first[j], first[i]));
}
}
// [s_first, s_last) are the sources of the sub-graph [s_first, last)
auto s_first = first;
auto s_last = s_first;
for (std::size_t i = 0; i < n; ++i) {
if (in_degree[i] == 0) {
std::swap(first[i], *s_last);
std::swap(in_degree[i], in_degree[s_last - first]);
++s_last;
}
}
for (; s_first != s_last; ++s_first) {
for (auto t_it = s_last; t_it != last; ++t_it) {
if (edge(*s_first, *t_it) && --in_degree[t_it - first] == 0) {
std::swap(*t_it, *s_last);
std::swap(in_degree[t_it - first], in_degree[s_last - first]);
++s_last;
}
}
}
}
Kahn’s algorithm runs in O(|V| + |E|) time, where |E| is the number of edges.
For a dense graph, |E| ~ |V|^2, therefore our algorithm runs in O(|V|^2).
Afterword
We showed that why std::sort cannot be used for topological sorting,
and then implemented topological sorting under a similar API.
Perhaps, a few more finite graph algorithms can be implemented in this flavor:
template <class RandomIt, class F>
RandomIt find_cycle(RandomIt first, RandomIt last, F edge);
template <class RandomIt, class F, class V>
void depth_first_search(RandomIt first, RandomIt last, F edge, V visitor);
...
Am I dreaming std::graphs? Maybe one day. Maybe.